首页 > 行业动态
从获取全球导航卫星系统(Global Navigation Satellite System, GNSS)站观测数据,到站坐标归算至CGCS2000,需要经历基准站选取、数据处理、站坐标归算等过程。首先,由于已知点选取的不同,后续处理站点基于的基准不同;其次,数据处理时如果采用国际高精度数据处理软件(GAMIT、BERNESE等),若站点较多,超过了软件允许的范围,需要进行分区处理,不同的分区策略也将对数据处理结果产生影响;再则,在获得平差站坐标后需要归算到CGCS2000,而归算方法的不同对结果会产生很大的影响。基于上述原因,本文主要介绍基于GNSS观测数据到CGCS2000归算过程中的优化策略,并和常规方法进行比较,同时就以上几个环节的不同策略和方法进行定性和定量分析,并给出实例和相关结论,供相关应用借鉴。
1 基准站选取
框架是坐标系的具体实现。基准站在框架维护中实际上起骨架作用,确定框架相对于理论定义坐标系的相对位置关系;基准站选取越科学,坐标系实现越精准。框架实现涉及基准站数量、基准站质量、基准站分布等内容。
1.1 基准站选取原则
本文主要基于国家基准网数据处理过程具体说明选取准则。首先利用全球框架站点时序等资料,按照国际通用标准,并基于以下原则对各测站的数据质量进行分析:①连续性原则,测站在近3 a(或以上)进行连续观测,剔除观测年数不够以及处理过程中不连续和观测质量较差的站点。②稳定性原则,站点坐标时序稳定性好,具有稳定“可知”的点位变化速度。③高精度原则,速度场精度优于3 mm/a。④多种解原则,至少3个不同分析中心的速度场残差好于3 mm/a。⑤平衡性原则,站点尽量全球分布。⑥精度一致性原则,站点的位置和速度的精度应当一致。
在此基础上,本文提出监督分类七参数法对测站进行精选[1-4]。在一个板块(或块体)上,各站的速度大小和方向应当基本一致,而且在空间上的变化应是逐渐的。本文采用的主要方法是以板块运动模型划分的板块边界作为地学资料。对于粗选取的框架点,首先将实测的(X, Y, Z)的速度(VX , VY , VZ )按式(1)转换为平面速度(Ve , Vn ),再根据式(2)拟合板块模型欧拉矢量参数(ω'x , ω'y , ω'z )。
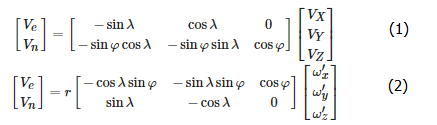
式中,r 为半径;( φ, λ )为站点的纬度、经度。
用求出的模型参数(ω'x , ω'y , ω'z )计算每个测站的速度,称为模型速度。同时计算速度矢量的方位角,将各站的模型速度和方位角与实测速度和方位角相比较,剔除残差项绝对值分别大于2σ1 和2σ2 的测站:
![]()
式中,σ1 为板块内测站模型速度残差的中误差;σ2 为方位角残差中误差;Λ为速度的方位角。
基于上述原则,在国际地球参考框架(international terrestrial reference frame,ITRF)站中选取了92个国际站作为框架站,这些站可作为我国基准框架数据处理的基准站,其分布见图 1。图 1中红色三角是采用监督聚类法选取的92个国际GNSS服务(international GNSS service, IGS)站。
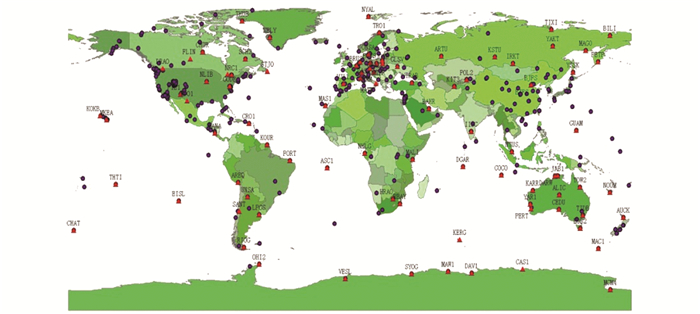
图 1 全球框架站点分布
1.2 测站分布均衡性评价方法
研究表明,测站的分布对计算结果会产生一定的影响,基准站分布均匀,可使参数估计更精确可靠。最小二乘平差方法一方面要求观测值要尽量多且精度要高,另一方面要求测站尽可能均匀地分布在整个稳定地区,使关系矩阵有较强的结构。在一个板块上,站点的分布一般是不均匀的,所以应根据站点覆盖面积最大、分布尽量均匀的原则来布站,这样不仅有利于卫星定轨,也可使基准构架更合理。基于以上考虑,本文提出了站点的分布均匀化评价准则。
理论上讲,如果选择的站点均匀分布在地球表面上,则求取网的重心坐标应该接近于坐标原点(地心),将此作为测站分布合理性评价指标,公式为:
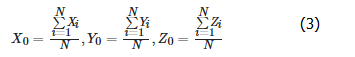
式中,(X0, Y0, Z0 )为重心坐标; N为测站数。
考虑到站点分布在地面上,不完全是理想的椭球面,受地面高低起伏的影响,X、Y、Z 满足上述条件比较难,因此将网的重心坐标转换成大地坐标。则评价标准为网的重心坐标经度应接近起始子午面,反映站点分布东西对称;纬度接近赤道,反映站点分布南北对称; 大地高接近地心。
2 分区方法及数据处理
2.1 间距分区与区域分区
1) 间距分区法
基准站观测共视卫星,观测数据中误差的相关性与站间距有关,随着站间距增大,相关性越来越弱。本文针对多基准站、密集型分布连续运行参考站(continuously operating reference stations,CORS)站网进行基线解算时需要分区,尤其是网中站间基线长度差异较大时的情况,提出了间距分区法[5-7]以提高解算精度。所谓间距分区法是根据各个测站之间的距离,将分布密集的测站抽稀,使距离较近的测站均匀地分布在不同的分区,尽量避免短基线,使基线长度比较均匀,以此来提高GAMIT软件对各测站基线解算的精度。用间距分区法进行基线解算,既考虑了测站间距的问题,保证各个测站间基线长度较长,又兼顾了测站分布状况,使得测站分布较为均匀。以图 2、图 3中某省CORS站为例说明间距分区法。
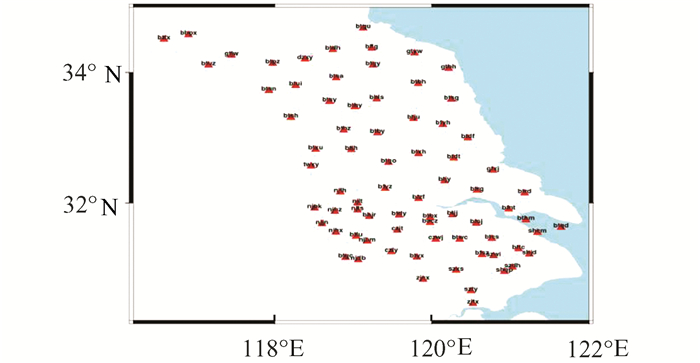
图 2 某省CORS站分布图
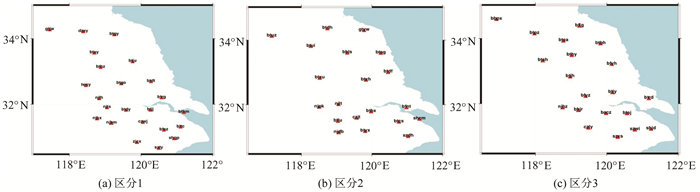
图 3 间距分区法划分的3个分区
2) 区域子网划分法
区域子网划分法是依据我国二级板块分布,结合各板块地理特征及测站分布情况进行划分的。也有按经纬度进行子网划分[8]。
2.2 分区方法与整体解算一致性分析
以陆态网(crustal movement observation network of China, CMONOC)基准站解算为例[6], 比较分析两种分区法与整体解算结果的差异。为保证能进行整网解算,选取全国55个陆态网络连续运行基准站2013年3 d的观测数据, 区域框架站采用7个中国及周边IGS框架站。分别采用整网解算方案以及两种分区方案进行解算,其站点分布情况如图 4所示。图 4中红色五角星表示IGS站,蓝色点表示陆态网连续运行基准站。
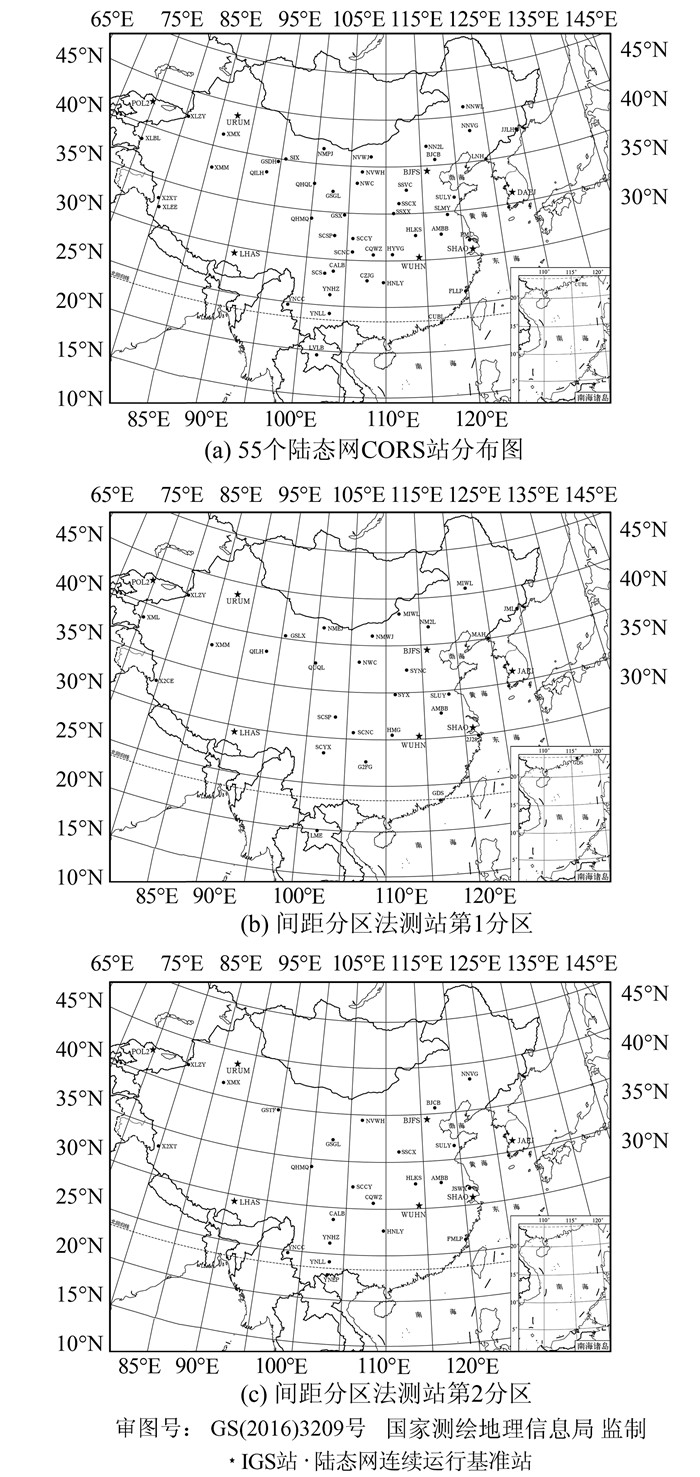
图 4 55个陆态网CORS站分布图及间距分区法测站分布示意图
图 4采用间距分区法将测站划分为两个区。图 5为采用区域子网划分法,依据中国二级板块划分及测站分布情况,保证每个板块有足够的站点。中蒙和中朝板块合并划为东北区,华北平原和鄂尔多斯板块合并划为华北区,鲁东-黄海、华南及南海板块划为华东区,天山及塔里木板块划分为新藏区,其他小板块合并为西部区,55个测站共划分为5个区。

图 5 区域子网划分法测站分布图
利用GAMIT/GLOBK软件进行解算,统计3种解算方案解得的基线长以及测站坐标,分析两种分区方案与整网解算方案的基线长度差及三维方向坐标差,并计算基线的相对精度。图 6为两种分区方案与整网解算方案作差求得的基线相对精度;图 7为两种分区方案与整网解算方案B、L、H 方向坐标差。
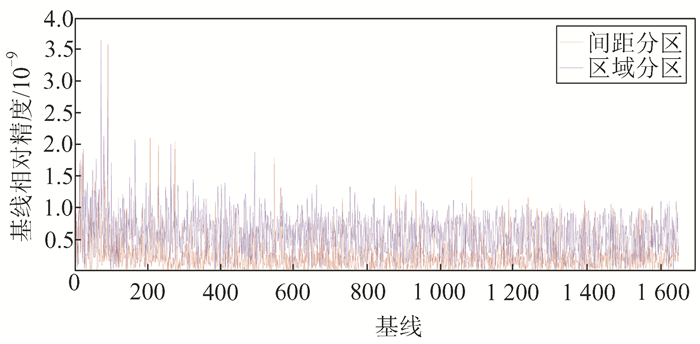
图 6 两种分区方案基线相对精度
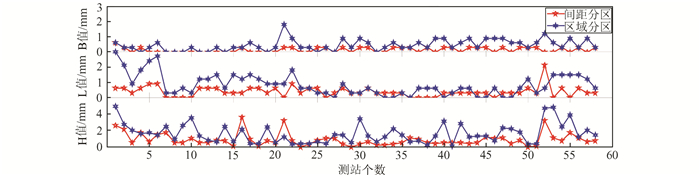
图 7 两种分区方案大地坐标系下坐标差
从图 6可以看出,间距分区法测区内基线相对精度明显高于区域子网划分法,间距分区方案解算精度高且稳定。从图 7可以看出,间距分区方案解算的测站坐标优于区域子网划分法,更加接近于整网解算方案,且精度均匀、稳定,三维方向坐标精度均优于2 mm;在大地坐标系下,水平方向的误差也基本上在1 mm以内,高程方向在2 mm以内。
2.3 陆态网数据处理
选取全国240个陆态网络连续运行基准站2013年1月共30 d的数据,同样采用两种方法分析解算结果差异:①间距分区法把测站均匀分布在6个测区;②基于板块按区域分区法分5个区。数据处理时采用我国及周边15个IGS框架站, 利用GAMIT/GLOBK软件进行解算及平差,计算得到全国GNSS连续运行基准站在ITRF2008框架、2013.04历元下的坐标。
区域分区方案南北分量的中误差平均值为±0.8 mm, 东西分量的中误差平均值为±1.0 mm, 垂直分量的中误差平均值为±2.6 mm。间距分区南北分量的中误差平均值为±0.5 mm, 东西分量的中误差平均值为±0.5 mm, 垂直分量的中误差平均值为±1.9 mm。图 8为240个陆态网络连续运行基准站采用间距分区法得到的N、E、U三个方向的坐标精度。
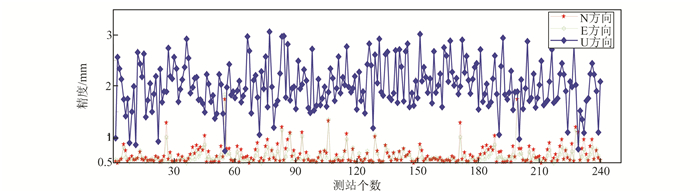
图 8 240个陆态网络连续运行基准站N、E、U方向坐标精度
从图 8可以看出,陆态网络连续运行基准站各测站解算结果在三维方向上的坐标精度均优于3 mm;在站心坐标系下,基准站解算结果在水平方向的误差均小于1 mm,高程方向的误差均小于3 mm。
3 板块运动改正
在获得了各站点坐标在ITRF框架、当前历元下的坐标后,需要将站点坐标归算到CGCS2000坐标系下,常用的做法一是采用强制约束平差的方法,即将CGCS2000的站作为平差基准,进行拟稳平差,二是采用速度场归算的方法[9-11]。通过两种方式将坐标改正到CGCS2000,并与这些站在CGCS2000下的坐标进行比较分析。为说明方法的不同,本文对原国家测绘地理信息局收集的2014年国际及全国省级近1 800个CORS站(包括国际92个IGS站)1个月的观测数据处理结果,采用两种改正方法将坐标改正到CGCS2000,与16个有CGCS2000坐标的国家基准站坐标进行比较,分析结果差异。
3.1 两种方法一致性检验
图 9是采用速度场归算的方法将ITRF2008框架下16个国家基准站在2014.664历元下的坐标归算到CGCS2000下,并与CGCS2000下的大地坐标基准差异进行比较,具体见图 9[11],图 9中差值单位换算成m。图 10为采用拟稳平差的方法强制归算的结果(N、E两方向)。
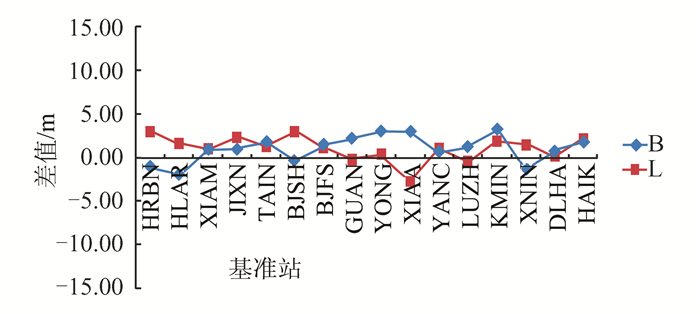
图 9 速度场归算后与已知值差异
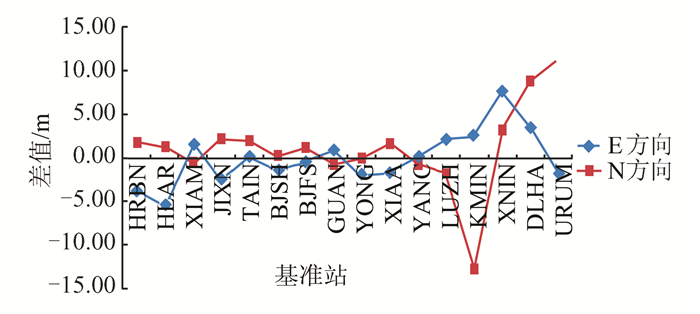
图 10 CGCS2000框架拟稳基准平差解与CGCS2000坐标的比较
从图 9、图 10中可以看出,整体上两种方法差异大的站点为XNIN、DLHA、KMIN、HRBN、HLAR。将这几个站按板块进行定位,其中XNIN、DLHA位于柴达木板块,KMIN位于川滇板块,HRBN、HLAR位于中蒙板块。这几个块体站的运动趋势与位于中原地区的其他各站差异较大,见图 11。从站的分布可以看出,中部地区站分布得比较密,约束平差在选取基准进行平差时,会基于用户指定的基准站组,根据赫尔默特七参数转换残差分析,选取运动趋势一致的基准站群作为拟稳平差基准。因此,与中原运动趋势一致的站点平差后结果与速度场归算结果较为吻合,而位于与中原趋势不一致的板块上的站点转换结果较差,达到分米量级。
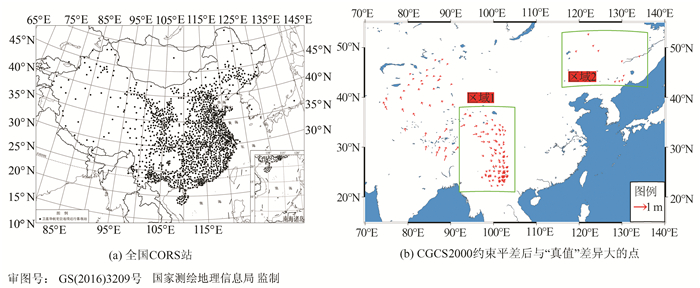
图 11 全国CORS站分布与CGCS2000约束平差后与真值差异大的站点分布图
3.2 结果比较分析
将全国各省级1 700多个CORS站按上面两种方法得到各测站在CGCS2000下的两套坐标求差,将各站N、E方向的差异表示成矢量,图 11为站点分布图及两种方法差矢量分布图。
图 11中只画出了与CGCS2000差异在分米量级(大于10 cm)的各站点的分布,对照速度场和板块模型可以看出,这些差异的走向和板块的运动方向一致,差异大的站都分布在东北、西北、川滇地区。平差后的整体网“回归”CGCS2000的趋势同所选基准网的分布、密度、运动趋势有关。在所选取的基准站网24个基准站中,中东部测站有10个站占了62%,且分布密度相对集中,决定了整体网的“走向”,因此差异大的点基本上都是和我国中部地区速度场走向不一致的点,即分布在东北、西北和华南川滇地区,这些区域基本上也是板块变形大的区域。约束平差由于未顾及板块运动趋势的不同,因此平差的结果较差。
4 综合结果分析
基于上述方法确定了我国1025个站点(剔除了只有一期观测数据和站坐标精度比较差的站点)的速度场,X、Y、Z速度场精度均方根(root mean square, RMS)由0.92、0.72、0.97 mm/a提高到0.19、0.45、0.32 mm/a。以这个速度拟合和建立了我国板块运动模型CPM-CGCS2000[12-13],并与国际上的ITRF2005、APKIM2005、PB2002、NUVEL1A[14-18]等模型进行比较,同时也与国内两种模型[19-20]进行比较。
图 12为BJFS、URUM、SHAO、WUHN这4个站各个模型归算后在经度、纬度方向与CGCS2000的差异。将文献[20]速度场模型称为CHINA_F,文献[19]计算的速度场为CHINA_W。由图 12可见,CPM-CGCS2000水平方向上比ITRF2005、APKIM2005、PB2002、NUVEL1A更加精确,与CHINA_F、CHINA_W两个模型相比,CPM-CGCS2000精度也更均匀,更能精确反映站点的水平运动。

图 12 各模型值与CGCS2000真值水平方向上的比较
5 结 语
确定GNSS观测站在CGCS2000下的坐标,不同的方法对最终结果都会产生很大影响[21-22]。不同于常规处理方法,针对GNSS网解算基准选取,本文提出了顾及板块运动因素的监督聚类基准站选取方法;针对密集型大网解算基线长度悬殊过大,提出了顾及站间误差传播相关性因素的间距分区方法;同时对于解算得到的当前历元下的站坐标归算到CGCS2000,提出了基于速度场的站坐标的归算方法。相较于传统的方法,本文方法能够提高整网的解算精度,速度场的精度也有很大提高,拟合的板块运动的精度也是目前国内精度最高的。
声明:登载此文出于传递更多信息之目的,并不意味着赞同其观点或证实其描述,文章内容仅供参考。
版权声明 : 本站部分论文来源于网络(或网友投稿),如有侵权,请联系我们删除处理。








